Introduction
The choice of which math curriculum to pick for a school district has major ramifications. Do you go with a modern curriculum that often forces students to write sentences, or do you go with something more traditional, where writing a sentence as an answer almost never happens? Or perhaps you want a happy medium between these two extremes?The Big Picture
What matters more than anything else is Algebra I readiness, and that foundation must be built properly in elementary school, starting as early as kindergarten or first grade. If your curriculum cannot do this, you might have failed before you've started!What is Algebra I Readiness?
If you do a web search and look at a few sites that talk about Algebra I readiness, you will get clear and consistent advice. By the time your students take Algebra I, they need to be good at the following:- Very strong at basic addition, subtraction, multiplication, and division
- Can add, subtract, multiply, and divide fractions with unequal denominators
- Can add, subtract, multiply, and divide negative numbers
Based on all of the conversations we've had with Algebra I teachers and math intervention teachers, these skills are a must, especially the ability to manipulate fractions. The bottom line is, if your students are not computationally very strong, they will not pass Algebra I.
In the ideal world, every Algebra I student will have deep critical thinking skills and computational excellence. This is especially necessary if you want to model a real world scenario as a set of algebraic equations. But let us take a step back and be realistic. The student that can consistently model a real world scenario as a set of algebraic equations and derive the right answer is going to get a solid A in Algebra I and will likely some day take AP Calculus. Today, it would be a monumental achievement if most of our at-risk students could merely pass Algebra I, which leads to this conclusion: Great critical thinking skills are highly desirable, but computation skills are a necessity.
What about the Common Core and all of those Tests?
On its own, the Common Core Standards are actually very well written and attempt to guide our students to have a deep understanding of mathematics as well as computational fluency. However, these standards do not explicitly dictate the way in which a deep understanding can be acquired. Today there are some very controversial methods being used to teach mathematics, and the Common Core is used as an excuse to use these methods. The truth is, the Common Core does not require this, so if you are attracted to some of the newest teaching methods, just know that you are doing this because you believe that is the best possible way to teach math, not because the Common Core says to do it (because it doesn't). If you want to verify this, read the Common Core Standards here.As for all the testing, that has proven to be a huge distraction. As already mentioned, the big picture is Algebra I readiness, which absolutely requires computational fluency. Because each grade level test must apply fairly equal weight to each individual standard, our priorities have become messed up. The standards that relate to computational fluency are therefore given less attention, which in the long run, leads to Algebra I failure.
Consider these charts, based on data from some California schools and the
California STAR test:
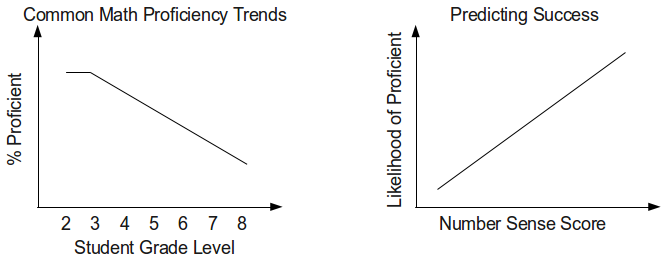
In the first chart, in high risk environments, student proficiency starts
to decline significantly in 4th grade and beyond. In the second chart,
we noticed a statistically significant correlation between score on
the Number Sense strand (focuses on computational fluency) and overall score. Our hypothesis
based on this data is that to score proficient on the STAR test as a 2nd or 3rd grader, a good computational foundation is not required, but once you hit skills like long subtraction in 4th grade and beyond, students that lack the proper foundation will fail.
If our analysis is correct, it suggests that insufficient time is being spent on computationally fluency in 1st, 2nd, and 3rd grade. The teachers don't even realize there is a problem because the standardized test scores for those grades are often pretty good. Without a deliberate and consistent change, this pattern will continue, regardless of the textbook series adopted by the school district.
How to Choose a Math Curriculum
Because there are so many math standards, if you faithfully cater to each math standard with equal emphasis, we find it highly unlikely that your at-risk students will be properly prepared for Algebra I when the time arrives, and your school district will have therefore failed.Our strong recommendation is to disproportionately pay attention to any skill that can be viewed as a building block toward fraction manipulation, and supplement your curriculum to make this possible. If you can find a textbook series that accomplishes this mission, then that is the curriculum you should adopt, and if your textbook cannot do this, find a good supplement.
Which Skills Build up to Fraction Fluency?
In order to be good at fractions, which makes Algebra I readiness possible, we recommend that your students achieve absolute mastery of the following skills by the end of each specified grade level:| Skill | Details | Target Grade |
|---|---|---|
| Understand the meaning of addition | Can relate addition to counting | Kindergarten |
| Addition math facts through 9 + 9 | Capable of getting 50 problems 100% correct within 2.5 minutes | 2nd grade (ideally 1st grade) |
| Understand the meaning of multiplication | Sees this as repeated addition. Furthermore, understands the commutative property, which is that 3 × 5 is equivalent to 5 × 3. | 2nd grade |
| Multiplication math facts through 9 × 9 | Capable of getting 50 problems 100% correct within 2.5 minutes | 3rd grade (ideally 2nd grade) |
| Understand the meaning of a fraction | Can relate fractions to visual models. Can visually understand why 2/4 is equivalent to 1/2. | 3rd Grade |
| Factoring and Prime Numbers | Can find all the factors for a number. Understand the meaning of prime numbers | 3rd Grade |
| GCF and LCM | Find the greatest common factor of two numbers. Find the least common multiple of two numbers. These skills are building blocks toward fraction simplification. | 4th Grade |
| Easy fraction addition and subtraction | Where denominators are the same | 4th Grade |
| Simplify fractions | Can simplify any fraction, including improper fractions and mixed numbers | 5th Grade |
| Add and Subtract Fractions | With unequal denominators, including mixed numbers | 5th Grade |
| Multiply and Divide Fractions | With unequal denominators, including mixed numbers | 5th Grade |
The first test comes with addition facts mastery by the end of second grade. This level of mastery is *very rare* among at-risk students by the end of second grade. In fact, in one our studies, less than 25% of all fifth graders we tested at a Title 1 school at the beginning of the year were proficient with their addition math facts. That needs to change. Get this brick in place by the end of second grade, and by the time these students get to fifth grade, they will be able to master all of their fraction concepts, and therefore be on track to eventually pass Algebra I.
Curriculum Recommendation?
If you choose a modern curriculum that focuses on critical thinking skills and forces students to write sentences as answers to some math problems, you will run into a brick wall of controversy and anger a huge percentage of your parents. That type of curriculum inevitably is very light on computation skills, so if you choose to go this route, you must deliberately supplement your curriculum based on the table above.If you choose a traditional curriculum, you will still have to supplement to ensure mastery of the addition and multiplication math facts. Your other point of emphasis is to focus on the "why" behind standard algorithms, which translates to understanding place value concepts deeply. You don't want your students to be computational robots that cannot critically think, so extra supplements involving real world scenarios may be necessary.
The point we'd like to make here is that regardless of your curriculum choice, you will have to supplement your students to ensure Algebra I readiness. Politically speaking, however, it's a lot less painful if your district chooses a traditional curriculum!
Is There a Good Supplement?
We thought you'd never ask :-)If you can consistently get your students on an Internet-connected computer 1 hour per week, we think you will have tremendous success with MathScore.com, and master all of the skills listed above on-time. We provide great supplemental practice for both computation skills and critical thinking skills, and of course we align to the Common Core standards (and others, including Texas).
