Introduction
If your child's math homework looks like nothing you've ever seen, and even worse, you aren't even sure how to answer it, you will be understandably frustrated, or possibly even downright angry (especially if you aced your math classes as a child). Let's first take a step back to understand why the homework looks the way it does.The Educator's Dilemma
The way math is taught is changing in the United States because a lot of people in the past failed with traditional methods, and because there are researched ideas that suggest better results. There is no proof that the new methods will produce a higher percentage of proficient students, so today's generation of students are effectively part of a huge educational experiment. We won't really know the results until your children are done with school.Rather than kick and scream, we recommend that you just accept today's reality and become curious to discover the potential benefits of today's approaches. If you have the means, by all means supplement your child with the math you were taught growing up. After all, once your child gets to Algebra I, the new methods are not needed.
The Goal of the New Methods
The high-level goal of the new methods is to produce a higher percentage of students that can apply mathematical concepts in real world situations. The fear is that in the past, we trained people to be more like robots that could compute things, but didn't understand why the math worked and often couldn't apply this knowledge in a useful real world context.If you take the perspective of grading a math homework assignment, any traditional worksheet will contain only numeric answers. Teachers would ask that you show your work so that they could get a sense for your critical understanding. With today's newer methods, the questions themselves will deliberately ask you to demonstrate a critical understanding, often by writing a sentence or two to explain things. In either case, you can argue that the teacher's goal is the same, which is to find out if you have achieved a critical understanding. The difference, however, is that in the past, some students could squeak by without a critical understanding, and today, there is no way to get around it.
But some of these methods look ridiculous to me!
Yes, sometimes they look ridiculous, and moreover, sometimes they look ridiculously inefficient. However, bear in mind that the real intent is not for the student to use this method on a regular basis, but to use this method merely as a tool to demonstrate a critical understanding. Once you are done with that unit, we highly recommend that you revert to standard algorithms, which by the way, are required by the Common Core standards.Sample Confusing Questions and Why They Exist
Before going through these exercises, we want to first point out that you cannot blame the Common Core standards for any of these questions. Curriculum providers are free to interpret the standards however they want, and it just turns out that many of them are using new approaches.Q. Show 3 different ways to add 9 + 8.
A.
- Draw a picture and count
- Add 1 to 9 and take away 1 from 8 to get 10 + 7, resulting in 17
- Memorize the answer
Why this problem?
The Common Core standards specifically want our students to have a strong understanding of place value concepts. The dream answer that the teacher wants to see here is answer #2, which takes advantage of base 10 concepts to arrive at a trivial problem to solve, which is 10 + 7. This can also visually be viewed as a "number bond", where the 8 (the whole) is broken into its parts, 1 and 7. The 1 is then grouped with the 9, forming a group of 10, resulting in 10 + 7. Here's the number bond picture:
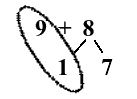
The reason why this problem looks appalling is the fact that the numbers being used are so small and trivial. A better question, in our opinion, would look like this:
Q. What would you do to solve 367 + 98 in your head?
A. I would see 98 as "100 - 2". 367 + 100 - 2 = 467 - 2 = 465
Now all of a sudden, the deep understanding of place value concepts feels much more practical, largely because unlike 9 + 8, you would never want to memorize the answer to 367 + 98.
Educationally, the main issue here is that the original problem would seem appropriate for a 1st grader, but our suggested problem involves larger numbers that might not seem appropriate for 1st grade. The standards, however, want the understanding of place value taught in 1st grade, so the creator of the question was forced to use smaller numbers.
In the old days, perhaps everybody could answer 9 + 8 correctly (because everybody memorized it), but not everybody could break down the problem as seen in the number bond picture. And that's the fundamental difference between the old ways and the new methods. All that being said, we believe that everybody still needs to master their math facts, so 9 + 8 must eventually be memorized by today's students.
Q. Multiply 24 × 56 using the lattice method
A.
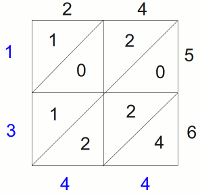
Therefore, 24 × 56 = 1344.
OK, you lost me, what the heck is going on?
For the most part, the computations used are no different from what you see in the standard algorithm. The major difference is that you first have to draw a box with a bunch of diagonal lines. Starting with the top left corner, you have 2 × 5 = 10. The next box on the right is 4 × 5 = 20. To get the final answer, you look along the diagonal lines and just add up the numbers.In the standard algorithm, some of your scratch work is written above the numbers and you might scratch out some of those numbers as you go along. In the lattice method, this type of scratch work disappers. Furthermore, in the standard algorithm, you must finish things off by doing long addition. In the lattice method, you are technically doing long addition at the end, but it does not feel like long addition.
For some people, the standard algorithm is confusing, and the lattice method is easier. You might not be used to the lattice method, but given our explanation, hopefully it won't be a stretch to understand it. Some teachers report that the majority of their students prefer the lattice method.
Quite honestly, our only objection to the lattice method is the fact that you have to draw a box with a bunch of lines, which takes time to set up. If the numbers to multiply are bigger, you have to draw even more lines. Anybody that is obsessed with answering questions rapidly will prefer the standard algorithm, and perhaps people that are a bit more patient might prefer the lattice method. If the lattice method appears to reduce confusion, go ahead and use it. Our reluctance to use it ourselves most likely stems from the fact that we weren't taught this method growing up.
Q. Multiply 24 × 56 using the box method (also known as grid method).
A.
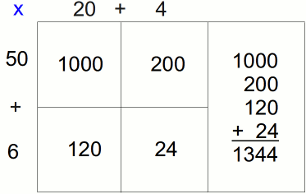
The box method and lattice method are extremely similar except that the box method directly forces you to think in terms of the actual value of the terms being multiplied. In the lattice method, you would think "2 × 5 = 10", but with this method, you would think "20 × 50 = 1000". Pause for a moment and think about how you would solve 24 × 56 in your head. We realize that not everybody is capable of solving this in their heads, but a good approach to solve this in your head would be to do precisely the operations required by the box method.
Our Opinion - Whereas the standard method and lattice method abstract away the notion of place value, this one directly forces you to confront it. From the standpoint of teaching students to really appreciate place value, we think this is a worthwhile alternate method for teaching long multiplication. Furthermore, students familiar with this method will be in good shape to do algebraic multiplication. For example, (2x + 3)(3x + 5) can be solved intuitively using the box method.
When it comes to pure speed, the standard algorithm reigns supreme and must be taught in order to align to the Common Core standards, but in terms of teaching place value, we really do think the box method is useful.
Q. Solve 412 - 186 using a number line.
A.

With a number line, subtraction is viewed as the distance between two points. This method turns subtraction upside down and turns it into an addition problem. It appeals to people who get confused with the standard algorithm because you don't have to cross out numbers or do any borrowing. Pause for a moment and try to compute 412 - 186 in yor head. If you are capable of solving this in your head, chances are, you will compute 200 - 186 = 14, then 412 - 200 = 212, then 212 + 14 = 226. In other words, the way you solve it in your head closely approximates the number line method. To solve this in your head using the standard algorithm is far more difficult, which is suggestive that only people with a deep understanding of place value will be able to solve this problem in their heads.
If you are quick to point out that the standard algorithm is a lot faster, we'll be quick to agree with you, but as stated before, that's not the point of this method. The real point of this method is to explicitly develop a critical understanding of place value, which has the side effect of making it easier for students to learn how to solve problems like these in their heads.
If you still aren't convinced, consider when you hand a $20 bill over to a cashier for a purchase of something that costs $3.67. The cashier does not always hand you a wad of bills and coins and say "Here's $16.33". Instead, the cashier first hands you 33 cents and says "4", then hands you a $1 bill and says "5", then hands you a $5 bill and says "10", then hands you a $10 bill and says "20". A noticeable percentage of cashiers provide change this way because the average person would rather add than subtract, which makes this method intuitive not only for the cashier, but for the customer as well. Some of us would greatly prefer for the cashier to hand us $16.33 and say "$16.33 is your change", but the fact is, clearly we don't all think the same way, and the reverse method of starting with the coins, then the $1 bill, then the $5, then the $10 is helpful for quite a few people.
Our opinion - Although it looks ridiculous at first glance, we believe the number line is a good supplemental method to teach subtraction to students because it does appear to develop critical understanding and will help students learn to solve such problems in their head. But after the understanding has been developed, the standard algorithm (which is required by the Common Core standards) reigns supreme and ought to be used.
